介绍
Trie树,又称为字典树、单词查找树或者前缀树,是一种用于快速检索的多叉树结构。比如小写英文字母的字典树是26叉数,数字的字典树是10叉树。
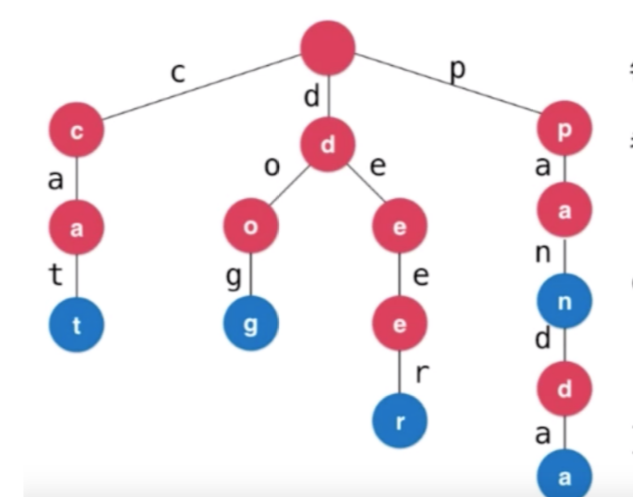
Trie树的基本性质有三点,归纳为:
- 根节点不包含字符,根节点外每一个节点都只包含一个字符
- 从根节点到某一节点,路径上经过的字符连接起来,为该节点对应的字符串。
- 每个节点的所有子节点包含的字符不相同(分叉)
Trie树从根节点到某一节点,都可以称为一个字符串,但是不一定是单词。比如图中在没有添加pan这个单词的时候,pan 只是 panda的前缀,一个普通字符串. 只有在添加pan这个字符串之后,pan这时候才是一个单词。
代码实现
在这里我使用了节点TreeMap来保存父节点与子节点的映射关系。也可以使用HashMap或者当字符数量固定的时候(比如就26个小写字母,那直接使用数组也是可以的)。
字典树从根开始不同的字符组成一条条的通路,而形成了一个树状结构1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79//字典树
public class Trie {
private Node root;
private int size;
public Trie() {
root = new Node();
size = 0;
}
//获取单词的数量
public int getSize() {
return size;
}
// 向Trie中添加一个新的单词word
public void add(String word) {
Node cur = root;
for (int i = 0; i < word.length(); i++) {
char c = word.charAt(i);
if (cur.next.get(c) == null) {
//说明当前没有c这个字符的分支 那么新建一个分支
cur.next.put(c, new Node());
}
// 不论是否包含c这个字段(不包含会新建分支) 那么树都要下一个深度(只是c这个分支)
cur = cur.next.get(c);
}
//cur到了这个单词的最后一个字符
if (!cur.isWord) {
//例如 先存在panda 添加pan
//或者先存在pan 在添加pan 这是不能再size ++了 因为已经存在此单词了
cur.isWord = true;
size ++;
}
}
// 查询单词word是否在Trie中
public boolean contains(String word) {
Node cur = root;
for (int i = 0; i < word.length(); i++) {
char c = word.charAt(i);
if (cur.next.get(c) == null) {
return false;
}
cur = cur.next.get(c);
}
//return true; 不能直接返回true 因为可能我们查的单词可能是前缀 但是不是我们前面添加的单词
// 比如只是添加了panda 不能说明pan 存在于Trie 因为我们从来添加过pan这个单词
return cur.isWord;
}
// 查询是否在Trie中有单词以prefix为前缀
public boolean startsWith(String prefix) {
Node cur = root;
for (int i = 0; i < prefix.length(); i++) {
char c = prefix.charAt(i);
if (cur.next.get(c) == null) {
return false;
}
cur = cur.next.get(c);
}
return true;
}
private class Node {
public boolean isWord; //是否是一个单词
public TreeMap<Character,Node> next;
public Node(boolean isWord) {
this.isWord = isWord;
next = new TreeMap<>();
}
public Node() {
this(false);
}
}
}
总结
字典树典型应用有:
- 字符串的快速查找:先把熟词建一棵树,读入一篇文章找出所有不在熟词表中的生词;
- 字典序排序:用字典树进行排序,采用节点数组的方式创建字典树,这棵树的每个节点的所有儿子。很显然地按照其字母大小排序,对这棵树进行先序遍历即可。
- 前缀的应用:被搜索引擎系统用于文本词频统计。它的优点是:利用字符串的公共前缀来减少查询时间,最大限度地减少无谓的字符串比较。搜索提示。如当输入一个关键词,可以自动搜索出可能的选择。
字典树它是一种树形结构的数据结构。之所以快速,是因为它用空间换时间,时间复杂度不跟单词的数量n有关,只跟查询单词的长度length有关系。在优化消耗大量空间问题上可延伸出字典树的变种,比如压缩字典树、三分搜索树等。