AnthonyZero's Bolg

数据结构-线段树

发表于 | 分类于

介绍

线段树（Segment Tree）是一种二叉树形数据结构，用以存储区间或线段，并且允许快速查询结构内包含某一点的所有区间。

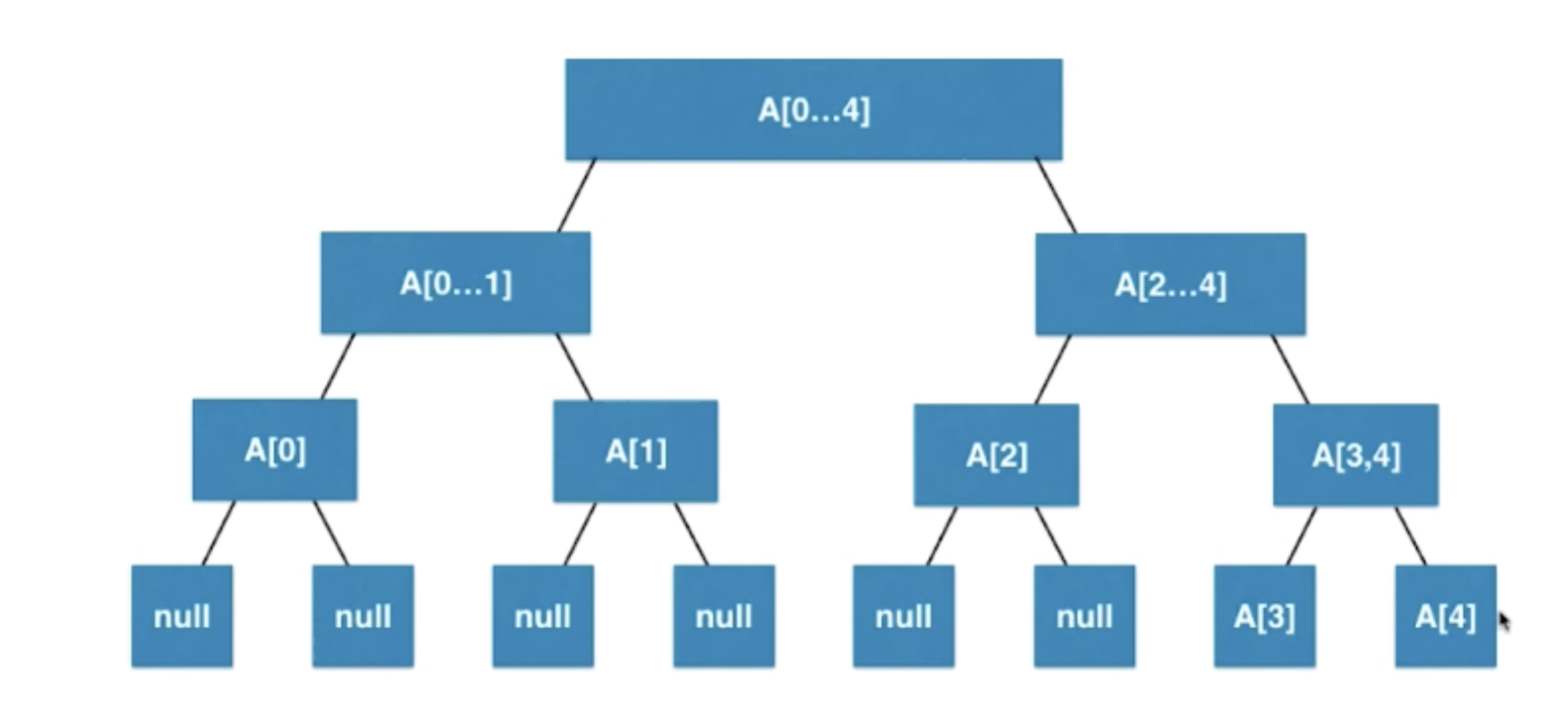
segementTree.png

  1. 线段树是一棵高度平衡的二叉树，有可能是满二叉树或者完全二叉树，但这不是必要条件
  2. 线段树的每一个结点都代表一个区间。父结点所代表的区间是两个子结点的融合。兄弟结点所代表的区间相互不重叠。根结点代表整个区间。
  3. 叶子节点对应原始数组中的元素
  4. 线段树不考虑添加元素，即区间固定。跟堆一样用数组表示，如果给定原生区间数组有n个元素，那么这个线段树的数组表示需要4n的空间

一个包含 n 个区间的线段树，空间复杂度为 O(n)，查询的时间复杂度则为 O(logn+k)，其中 k 是符合条件的区间数量。一颗线段树的构造就是根据区间的性质来构造的

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150

public interface Merger<E> {
    E merger(E a, E b); //怎么融合线段树两个区间 根据自己业务决定 可以是两个区间的和 或最大最小值等
}

public class SegmentTree<E> {

    private E[] tree;  //根据业务决定后 建立的线段树 的数组 保存每个区间的结果 4*data.length
    private E[] data;  //元素数据
    private Merger<E> merger;

    public SegmentTree(E[] arr, Merger<E> merger){
        this.merger = merger;

        data = (E[])new Object[arr.length];
        for(int i = 0 ; i < arr.length ; i ++)
            data[i] = arr[i];

        tree = (E[])new Object[4 * arr.length]; //4n容量

        // 从树根开始递归 根据原数据来构造 线段树 tree[0] tree[1] tree[2]
        buildSegmentTree(0, 0, data.length - 1);
    }


    // 在treeIndex的位置创建表示区间[l...r]的线段树
    private void buildSegmentTree(int treeIndex, int left, int right) {
        if (left == right) {
            //递归到底部 这里建立叶子节点 此时节点的值 就是原数据数组某个索引的值
            tree[treeIndex] = data[left];
            return;
        }

        int leftChildIndex = leftChild(treeIndex); //左子树所在tree数组中索引
        int rightChildIndex = rightChild(treeIndex); // 右子树所在tree数组中索引

        // int mid = (l + r) / 2 可能溢出;
        int middle = left + (right - left) / 2;
        buildSegmentTree(leftChildIndex, left, middle);
        buildSegmentTree(rightChildIndex, middle + 1, right);

        //根据业务来 merge可以求和 求最大值等等  从这里递归返回的过程 就是从底往上建树的过程
        tree[treeIndex] = merger.merger(tree[leftChildIndex], tree[rightChildIndex]);
    }

    public int getSize(){
        return data.length;
    }

    public E get(int index){
        if(index < 0 || index >= data.length)
            throw new IllegalArgumentException("Index is illegal.");
        return data[index];
    }

    // 返回完全二叉树的数组表示中，一个索引所表示的元素的左孩子节点的索引
    private int leftChild(int index){
        return 2*index + 1;
    }

    // 返回完全二叉树的数组表示中，一个索引所表示的元素的右孩子节点的索引
    private int rightChild(int index){
        return 2*index + 2;
    }


    // 返回区间[queryL, queryR]的值 data数组范围内
    public E query(int queryL, int queryR){

        if(queryL < 0 || queryL >= data.length ||
                queryR < 0 || queryR >= data.length || queryL > queryR)
            throw new IllegalArgumentException("Index is illegal.");

        return query(0, 0, data.length - 1, queryL, queryR);
    }

    // 在以treeIndex为根的线段树中[l...r]的范围里，搜索区间[queryL...queryR]的值
    private E query(int treeIndex, int l, int r, int queryL, int queryR) {
        if (l == queryL && r == queryR) { //到达叶子节点
            return tree[treeIndex];
        }

        int mid = l + (r - l) / 2;
        // treeIndex的节点分为[l...mid]和[mid+1...r]两部分
        int leftChildIndex = leftChild(treeIndex);
        int rightChildIndex = rightChild(treeIndex);

        if (queryL >= mid + 1) {
            //要搜索的区间都落在右边
            return query(rightChildIndex, mid + 1, r, queryL, queryR);
        } else if (queryR <= mid) {
            //要搜索的区间都落在左边
            return query(leftChildIndex, l, mid, queryL, queryR);
        } else {
            //要搜索的区间 在左右两边的区间都有
            E leftResult = query(leftChildIndex, l, mid, queryL, mid);
            E rightResult = query(rightChildIndex, mid + 1, r, mid + 1, queryR);
            return merger.merger(leftResult, rightResult);
        }
    }

    // 将index位置的值，更新为e
    public void set(int index, E e){

        if(index < 0 || index >= data.length)
            throw new IllegalArgumentException("Index is illegal");

        data[index] = e;
        set(0, 0, data.length - 1, index, e);
    }

    // 在以treeIndex为根的线段树中更新index的值为e
    private void set(int treeIndex, int l, int r, int index, E e){

        if(l == r){
            tree[treeIndex] = e;
            return;
        }

        int mid = l + (r - l) / 2;
        // treeIndex的节点分为[l...mid]和[mid+1...r]两部分

        int leftTreeIndex = leftChild(treeIndex);
        int rightTreeIndex = rightChild(treeIndex);
        if(index >= mid + 1)
            set(rightTreeIndex, mid + 1, r, index, e);
        else // index <= mid
            set(leftTreeIndex, l, mid, index, e);

        // 在线段树上index上面的各个线段 同时也要更新
        tree[treeIndex] = merger.merger(tree[leftTreeIndex], tree[rightTreeIndex]);
    }

    @Override
    public String toString(){
        StringBuilder res = new StringBuilder();
        res.append('[');
        for(int i = 0 ; i < tree.length ; i ++){
            if(tree[i] != null)
                res.append(tree[i]);
            else
                res.append("null");

            if(i != tree.length - 1)
                res.append(", ");
        }
        res.append(']');
        return res.toString();
    }
}