前言
堆(Heap)是一个可以被看成近似完全二叉树的数组。树上的每一个结点对应数组的一个元素。除了最底层外,该树是完全充满的,且最底层尽可能地从左到右填入。
堆我们可模拟看成是一颗完全二叉树,但是它底层数据结构是数组(完全二叉树是满二叉树的一部分, 不满的那一部分一定是树的右下部分)。而满二叉树是一颗除了最底下一层叶子结点外,其他节点都有左右子树。
堆包括最大堆和最小堆:最大堆的每一个节点(除了根结点)的值不大于其父节点值;最小堆的每一个节点(除了根结点)的值不小于其父节点值。
堆常见的操作:
- HEAPIFY 建堆:把一个乱序的数组变成堆结构的数组,时间复杂度为 O(n)。
- HEAPPUSH:把一个数值放进已经是堆结构的数组中,并保持堆结构,时间复杂度为 O(log n)。
- HEAPPOP:从最大堆中取出最大值或从最小堆中取出最小值,并将剩余的数组保持堆结构,时间复杂度为 O(log n)。
- HEAPSORT:借由 HEAPFY 建堆和 HEAPPOP 堆数组进行排序,时间复杂度为 O(n log n),空间复杂度为 O(1)。
堆结构的一个常见应用是建立优先队列(Priority Queue)。
概念
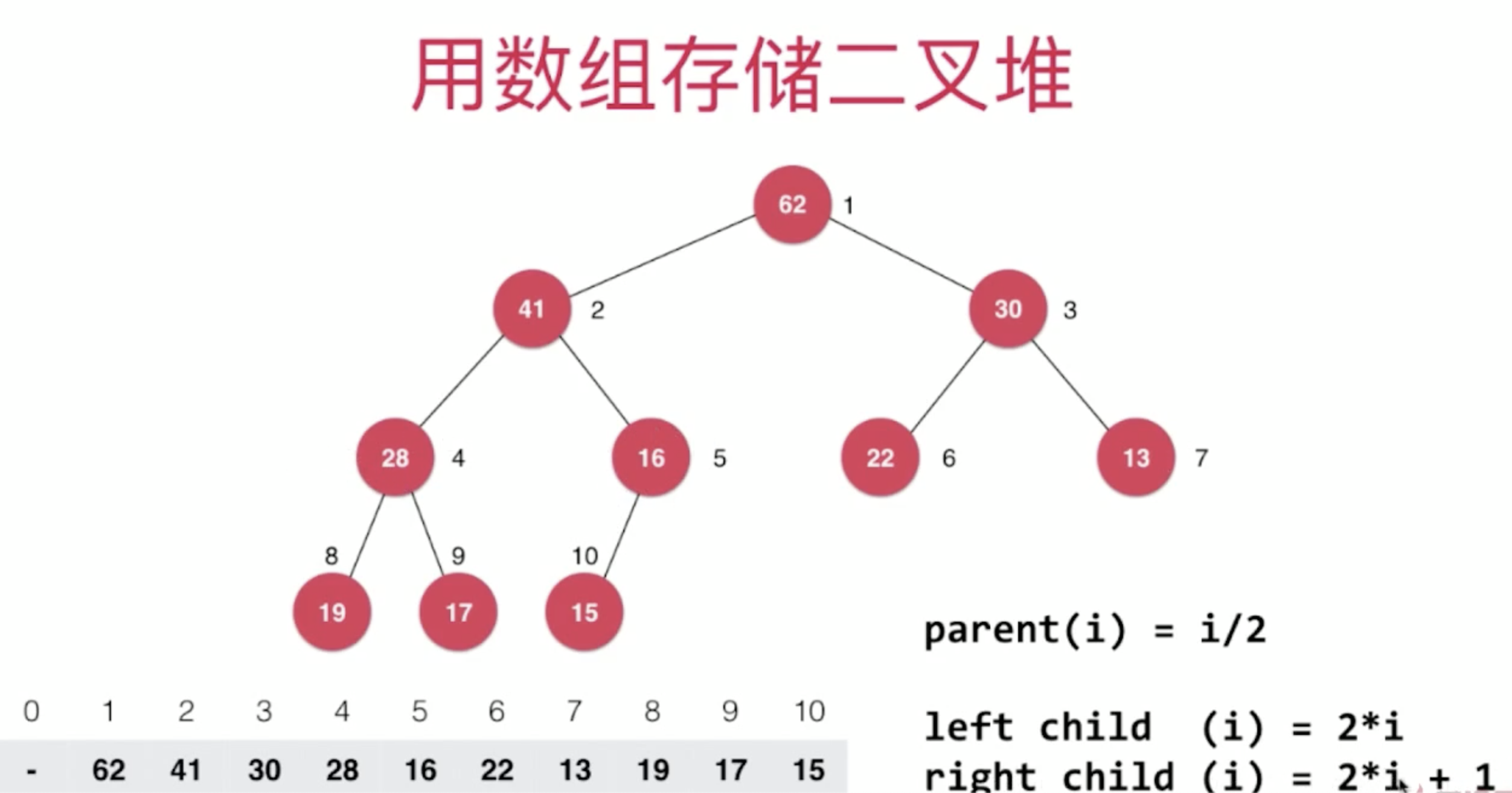
堆,有两种形式,一种是最大堆,另一种是最小堆。当然也可以扩展到k叉堆。如上图是一个最大堆,树根是最大值。
如果从数组的第一个节点开始存放数据的话,当前节点的父节点、左孩子、右孩子的索引就会有如下的关系:跟图中有区别:
parent(i) = (i - 1) / 2
Left child(i) = 2 * i + 1
Right child(i) = 2 * i + 2
父节点和孩子节点的父子关系通过数组下标来确定
堆基础
1 |
|
添加元素
为了维持堆的性质(完全二叉树),添加元素时,我们先将元素添加到数组的末尾,然后将该元素循环的与它父节点比较大小,比父节点大(这里假设是最大堆)就与父节点交换位置,跑到父节点的位置,之后就继续与新的父节点比较大小,直到小于等于父节点结束。这个过程叫上浮,
比如来个元素36比父节点16大,那么交换36和16在数组中的位置,此时继续看36的父节点41比它大,那么就结束循环了。实现如下:
1 |
|
删除元素
理解了插入的实现,删除也是遵循同样的规则。这里如图如果删除了堆顶元素62,那么为了维持完全二叉树的特性,我们很容易想到用最后一个元素15去替代这个62,替换完了没有完,此时15不满足都大于左右孩子的值,那么就要看它左右孩子的值哪个最大(这假设是最大堆),就跟它41替换跑到对应子树的位置,不断循环替换,直到没有孩子比他大的过程,称之为下沉操作:
1 |
|
依次删除堆顶元素是一个排序结果。如果是最大堆那么这个结果就是从大到小。
Replace操作
Replace是指将堆中的最大元素取出,替换另一个进去。可以直接将堆顶元素替换以后执行sift down操作
1 | // 取出堆中的最大元素,并且替换成元素e |
Heapify操作
Heapify是指将数组转化为堆
这里我们先将数组直接看成是一个完全二叉树,然后找到这棵二叉树的最后一个非叶子节点的节点,也就是该树的最后一个节点的父节点。然后从这个节点开始到根节点结束,执行sift down操作。1
2
3
4
5
6//heapify操作:将数组转化为堆
public MaxHeap(E[] arr){
data = new Array<>(arr);
for(int i = parent(arr.length - 1) ; i >= 0 ; i --)
siftDown(i);
}
完全二叉树的最后一层非叶子节点,从右往左,从下往上开始进行下沉sift down操作