题目描述
给定一个链表,返回链表开始入环的第一个节点。 如果链表无环,则返回 null。
为了表示给定链表中的环,我们使用整数 pos 来表示链表尾连接到链表中的位置(索引从 0 开始)。 如果 pos 是 -1,则在该链表中没有环。
说明:不允许修改给定的链表。
示例1:1
2
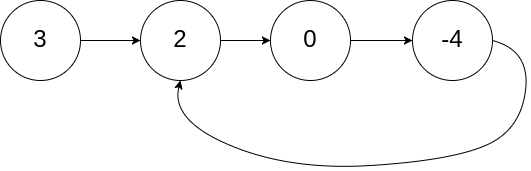
3输入:head = [3,2,0,-4], pos = 1
输出:tail connects to node index 1
解释:链表中有一个环,其尾部连接到第二个节点。
示例2:1
2
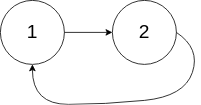
3输入:head = [1,2], pos = 0
输出:tail connects to node index 0
解释:链表中有一个环,其尾部连接到第一个节点。
示例3:1
2
3输入:head = [1], pos = -1
输出:no cycle
解释:链表中没有环。

进阶:
你是否可以不用额外空间解决此题?
思路
常规思路而言可以用一个 Set 保存已经访问过的节点,遍历整个链表并返回第一个出现重复的节点。由于使用了Set导致空间复杂度为O(n)。
为了降低空间复杂度,我们可使用快慢指针slow,fast。一开始都指向head。然后slow每次走一步,fast每次走两步。走着走着,如果fast变为空或fast的下一节点为空,说明链表无环。
当slow==fast时,说明有环存在。因为只有环时,slow才能赶上fast。否则slow永远在fast的后面。
此时head和fast每次一步,同时向前走,直到head和fast再次相等。相等的位置就为环的入口。
为什么head到环的入口距离 就等于 环内相遇点到环入口的距离?
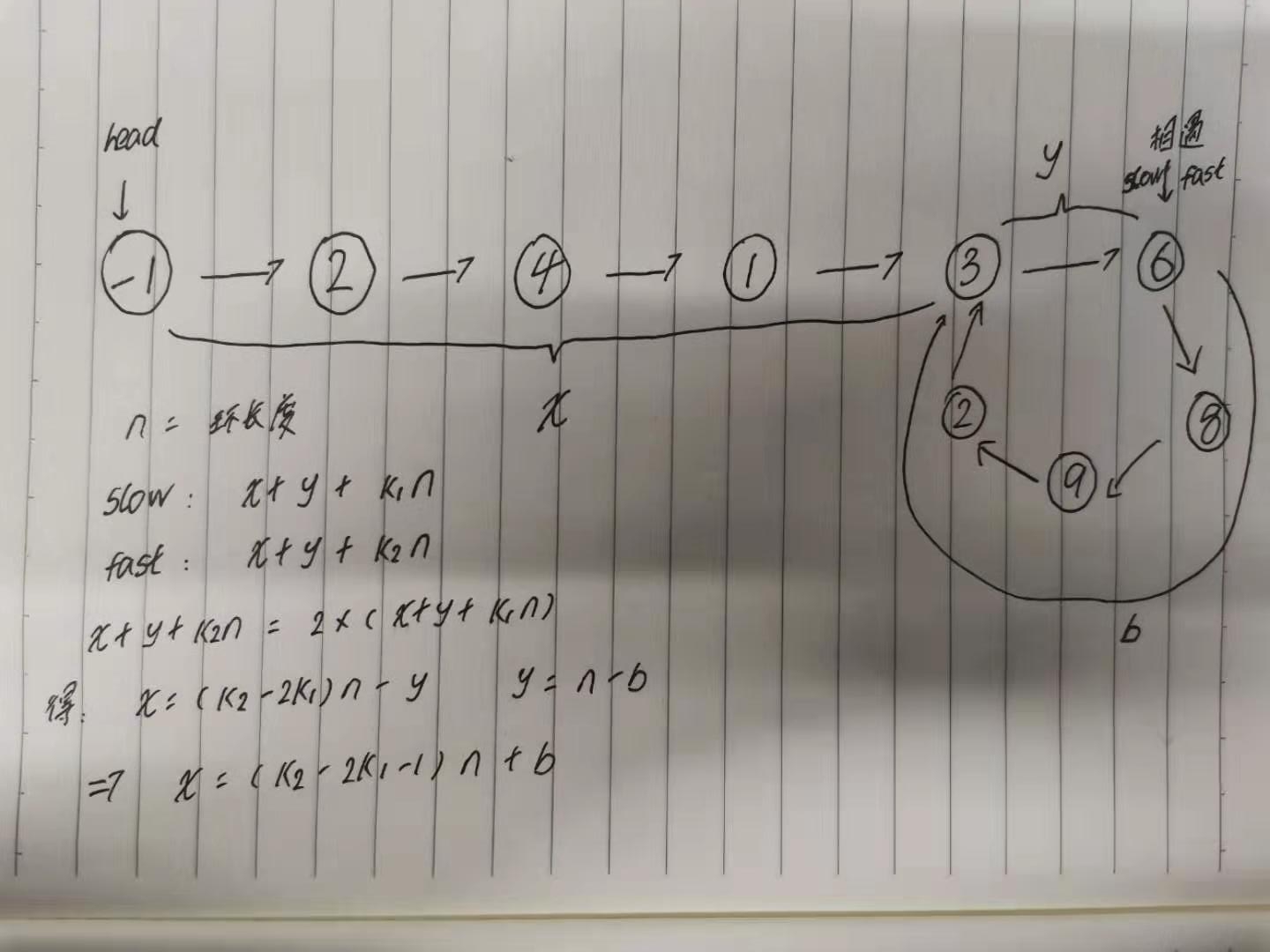
我们可以来证明:设
- x = head到入口点的距离 (图中-1 到 3)
- y = 入口点到相遇点的距离(相遇点肯定在环内) (图中3 到 6)
- b = 相遇点到入口点的距离 (图中6 到 3)
- n = 环长度
那么两个相遇时各自走过的长度为:
- slow走的距离为 x+y+k1n(k1是slow在环内走的圈数)
- fast走的距离为 x+y+k2n(k2是fast在环内走的圈数)
因为fast的速度是slow的2倍,所以他们走的距离的关系是:x+y+k2n=2*(x+y+k1n)
移项:x = (k2 - 2k1)n - y, 因为y = n - b代入左边式子
最后得出 x = (k2 - 2k1 - 1)n + b
所以当fast在相遇点,head和fast同时以1步的速度前进时,fast会转(k2-2k1-1) 圈整环,再走 b 步后与head一定终会相遇在环的入口。
(k2-2k1-1) >= 0
时间复杂度:O(n)
空间复杂度:O(1)1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24public ListNode detectCycle(ListNode head) {
if (head == null || head.next == null) {
return null; //没有环返回null
}
ListNode slow = head;
ListNode fast = head;
while(fast != null && fast.next != null) {
slow = slow.next;
fast = fast.next.next;
if (slow == fast) {
break; //停留在相遇点 环内 slow和fast
}
}
if(slow != fast) { //没相遇返回null 代表没环
return null;
}
//有环 寻找环的入环第一个节点
while (head != fast) {
head = head.next;
fast = fast.next;
}
return head;
}
代码地址见:Github, 一起来打好数据结构和算法的基础 (^▽^) 求star